刚体模拟与破碎

前言

几年前学完了GAMES103，跟着理了一遍图形学常用的刚体，布料，柔体，流体，算是入门了图形学的物理模拟，但之后呢？之后的路就得自己去探了，个人偏向追求实时计算以及视觉真实的游戏业界（毕竟感觉目前学界沉迷各种炼丹优化，或者拼接几种方法水论文），故打算重新审视下这几种模拟基本物体，看能否更进一步。

刚体模拟

冲量法

先热个身整下刚体模拟相关，对于刚体各引擎普遍采用线角速度更新，冲量处理碰撞(稳定，动量守恒)。大致流程如下图所示，感觉也不用多加赘述。

形状匹配

相较而言形状匹配在游戏引擎中没怎么用到，其优势场景应该是在不同类物体交互(刚体，布料，柔体，流体混杂)的物理引擎(Flex)。不过考虑到PBD系列也是这个思路(先自由更新，再约束投影)，也搓来玩玩当复健了。形状匹配大致思路就是先自由更新每个顶点，再最小化均方误差使其变为原形状(约束投影)。

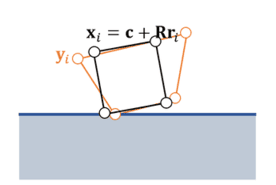
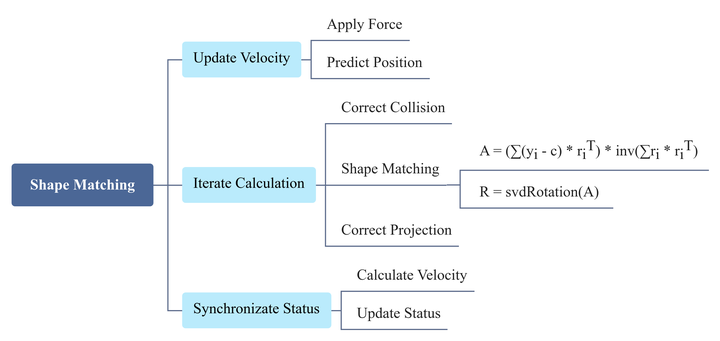
在算法流程中值得说道下的也就形状匹配部分，首先由物体当前状态，我们可以得到协方差矩阵$S=∑(y_i−c)⋅r_i^T$ ，再由协方差矩阵和预计算的参考形状的协方差矩阵($Q= ∑r_i⋅r _i^T $)的逆计算得到最优变换矩阵$A$，最后将最优变换矩阵$A$按$A=U\sum{V}^T$进行SVD分解，而最优旋转矩阵$R=UV^T$则在$A$基础上除去缩放和剪切得到。

刚体破碎

业内方案

刚体模拟总的来说难度不算很大，往深处整的话就可以试试刚体破碎相关，应用场景大概主要是FPS这种破坏地形能带来较大战略价值的游戏。开整之前，肯定是收集下相关技术分享以及成熟插件，看看现在业界的做法。技术分享中个人找到了GDC2015 Smash Hit的面切法，GDC2016 Rainbow6的固定模式破坏法，GDC2024 TheFinals的预分割冲量阈值分离法，GDC2025 Epic分享的预分割重合面积分离法。成熟插件方面个人找到了Unity的OpenFracture以及RayFire，UE的话Chaos原生就包含了倒是省了不少功夫。

GDC2015 Smash Hit面切

Smash Hit(弹珠冲击)算是童年回忆了，Gustafsson物理游乐场的游戏设计理念深得我心，这人干的Sprinkle(超级救火队), Smash Hit(弹珠冲击), Teardown(拆迁)也是真的帅。在弹珠冲击的破碎中，他使用双边数据结构，显式维护顶点、边、面的拓扑关系；动态边界体积树加GJK算法做碰撞检测；基于顶点分侧、边交点和封闭几何进行切割。

GDC2016 Rainbow6的程式破坏

在彩六中，育碧蒙特利尔工作室使用了RealBlast以进行程序性破坏。典型物件被拆为叶子图结构方便破坏。

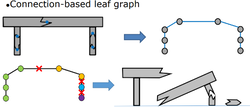
而墙面等则是先投影为二维，再由输入和材质参数产生特定形状，最后做多边形裁切和三角化。

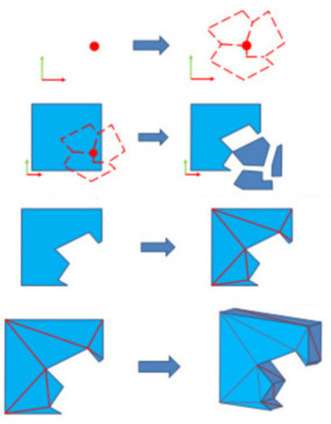
以及插播下分享的后半段都是关于网络同步和优化的，感兴趣的话可以找来看看。

GDC2024 TheFinals冲量阈值 & GDC2025 Epic重合面积分离

这两个放一起说，因为它们起点都是预分割网格，只是在分离逻辑上前者采用冲量阈值，后者采用了重合面积(一个应力一个应变倒也挺对称的，并且我都没找到能很好描述相关方法的图)。稍微展开一点的话前者是使用 Niagara 的 Mesh Renderer 和自定义 UV 集，在材质内部添加动画，再通过设置冲量阈值实现动态破碎；后者利用应变评估和锚定，通过比较碰撞形状与预分割图的重合程度实现动态破碎。

Unity插件及UE Chaos

(检测到相同框架，继续合批)。总体来说两个引擎对于实时切割基本只有随机面切，而预处理的话选择就丰富了许多，但大多数的原理还是Voronoi图。大致概念为生成一组点，再通过三角剖分等一系列操作给每个点分配一定区域。UE的均匀破碎，群集破碎和辐射破碎均是基于Voronoi图，只是生成点的逻辑各异罢了。

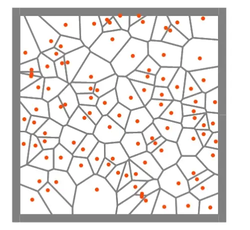
自设模拟

在看了一圈业内方案后，也是时候整些自己的解了。个人喜欢Smash Hit那种实时切割破碎的效果，但纵观所有方法，除了这个和彩六RealBlast的墙体方案，其他切割都是随机/预设而与碰撞信息无关。彩六的“由输入和材质参数产生特定形状”这步直接劝退，那就魔改下Smash Hit的相关方法吧。

数据结构

Gustafsson使用的双边数据结构显式维护顶点、边、面的拓扑关系。点很好理解，边和面的话则是因为每次切割都会在边上开出新的点切出新的切面。双边结构还是有些费了，可能Gustafsson基于封闭几何进行切割所以才需要这，但如果切割逻辑走三角剖分与顶点去重的话存储的网格结构就相对简单了不少。

struct MeshVertex{ float3 position, normal; float2 uv; }
class MeshEdge{ int v1, v2, t1, t2, t1Edge; }
class MeshData
{
    List<MeshVertex> vertices, cutVertices;
    List<int>[] triangles; public List<MeshEdge> constraints;
    int[] indexMap; int vertexCount, triangleCount
}

切割方法

正如前面数据结构中提到的，项目以三角剖分实现简化切割，大致流程如下：

顶点分侧：将顶点分为切割平面上方(topSlice)和下方(bottomSlice)两组。
边交点计算：对被切的边，插值计算交点，生成切割面顶点并添加到切面点集(cutVertices)。
三角剖分：三角剖分点集(cutVertices)和约束边(constraints)。
顶点去重：合并重复的切割面顶点(WeldCutFaceVertices)，消除冗余顶点。

其中最难的部分当属三角化，使用分箱排序后逐点插入的Delaunay三角剖分实现。项目干了几百行，不适合全贴出来这里就简单介绍下基本流程。

// 输入：顶点列表、约束边列表   输出：三角形索引列表
static List<int> Triangulate(List<MeshVertex> vertices, List<MeshEdge> constraints, Vector3 normal)
{
    // Step 1: 将3D顶点投影到2D平面（基于法线方向）
    List<TriPoint> points = ProjectVerticesTo2D(vertices, normal);
    // Step 2: 构建初始超级三角形（包含所有点）
    List<Triangle> triangles = CreateSuperTriangle(points);
    // Step 3: 插入所有点并逐步构建Delaunay三角网格
    foreach (TriPoint p in points) InsertPoint(p, ref triangles);
    // Step 4: 插入约束边并修复三角网格
    foreach (MeshEdge edge in constraints) InsertConstraint(edge.v1, edge.v2, points, ref triangles);
    // Step 5: 移除与超级三角形相关的无效三角形
    RemoveSuperTriangle(triangles, points);
    // Step 6: 转换为输出格式（顶点索引列表）
    return ConvertToIndexList(triangles);
}

碰撞响应

最后就是各凭本事的碰撞响应部分了，随机碰撞切割是真的每次随机位置随机角度干个切面，物理全靠之后的速度分配。折腾一番后想出三个物理近似的trick，也算是创了点新吧，其一为碰撞速度越快碎片越小，对应冲击强度越高，材料破碎越彻底。其二为碰撞点越靠近边缘越容易半切，对应边缘脆断的局部裂解。其三为以随机角度内倾切面，对应模拟应力沿最大剪切方向向内破裂。

大概做法为先根据碰撞点距中心以及边缘的距离确定此次是全切还是半切，再将网格顶点投影至与碰撞速度垂直的平面，以碰撞投影点和随机角度构造初始割线，接着从所有网格投影点中找到离该线距离最远的点，按切割比例把初始割线向该点移。再在世界空间(处理物体的缩放)下应用内倾角度补全切割线信息得到切割面。叙述起来不算复杂，但实操中还是踩了不少坑(比如最开始粗切割是轴对称矩形缩放为正方形再在单位内接圆边上按面积比例取两点切，细切割拿二维凸包计算面积比例。以及处理内倾时被Unity函数误导了好久，回想起渲染时法线的左乘转置逆矩阵才得解)，不知道能不能拿去水硕士毕业论文。

// 主代码中异步流程
IEnumerator FractureAsync(Collision collision)
{
    point = collision.GetContact(0).point; normal = collision.relativeVelocity.normalized;
    //切割比例，为避免极端效果取0.5上下浮动0.2
    sliceRate = 0.5f + 0.2f * (math.clamp((collision.relativeVelocity.magnitude - collisionVel.x) / (collisionVel.y - collisionVel.x), 0, 1) - 0.5f);
    while (fractureCount-- > 0)
    {
        MeshProjector.GetSlice(meshData, transform, point, normal, sliceRate, sliceTilt,
            out var sliceNormal, out var sliceOrigin, out var isFullSlice);
        MeshSlicer.Slice(meshData, sliceNormal, sliceOrigin, out var topData, out var bottomData);
        meshes.Add(bottomData.ToMesh());
        topMass = remainMass * (isFullSlice ? 1 - sliceRate : sliceRate);
        bottomMass += remainMass - topMass; remainMass = topMass;
        if (isFullSlice) CreatFragment(bottomMass); meshData = topData; //全切直接生成碎片，半切保留
        yield return null;
    }
    if (meshes.Count > 0) CreatFragment(bottomMass); gameObject.SetActive(false); //先生成一个，避免全半切仅一个碎片的情况
    remainData = meshData; meshes.Add(remainData.ToMesh()); CreatFragment(remainMass);
}