GAMES201
Lec1 课程介绍
基于物理的动画简介

物理引擎及应用
定义:在电脑中模拟真实世界

应用:计算机辅助设计,电影特效,VR/AR,训练机器人,游戏

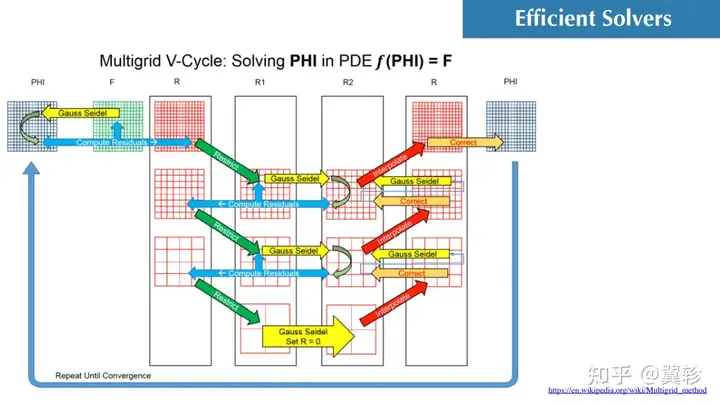
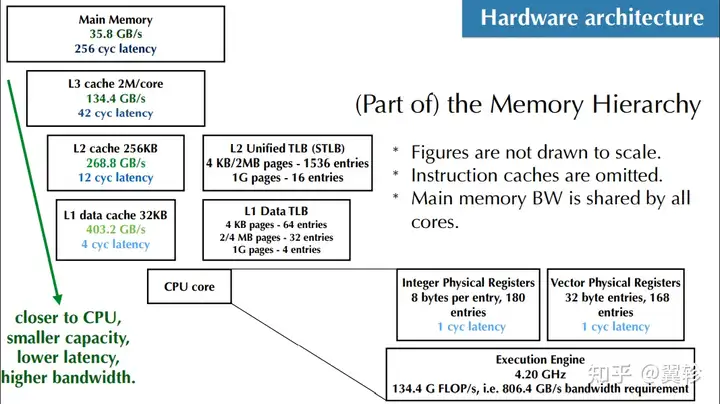
课程关键词
离散化、高效求解器、生产力、性能、硬件体系结构、数据结构、并行化、可微编程





Taichi 编程语言简介
什么是太极

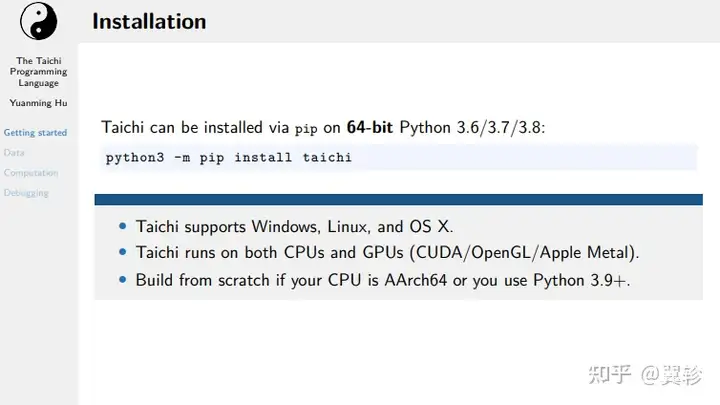
太极的安装
太极的初始化

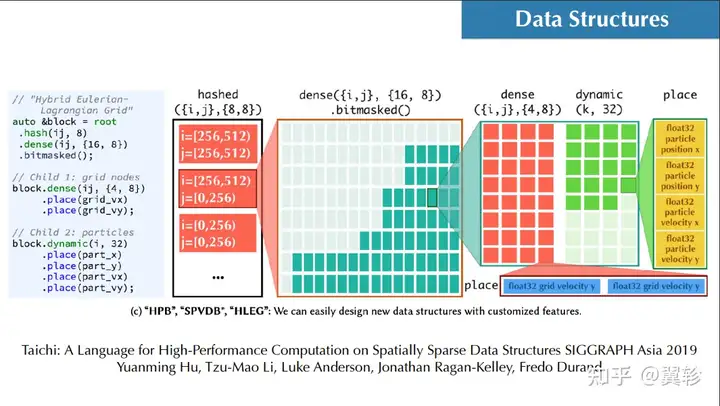
太极的数据结构
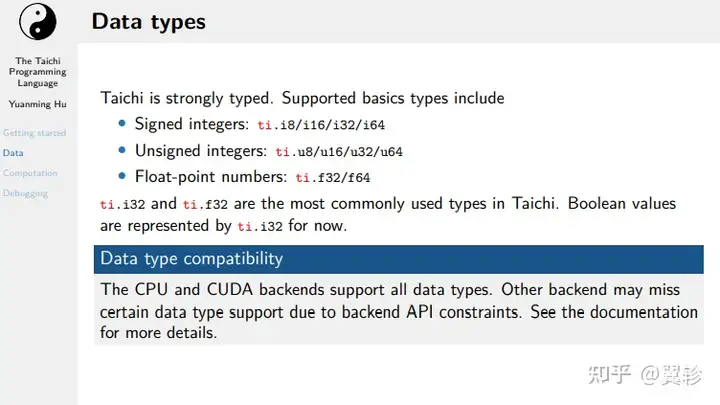
太极的张量
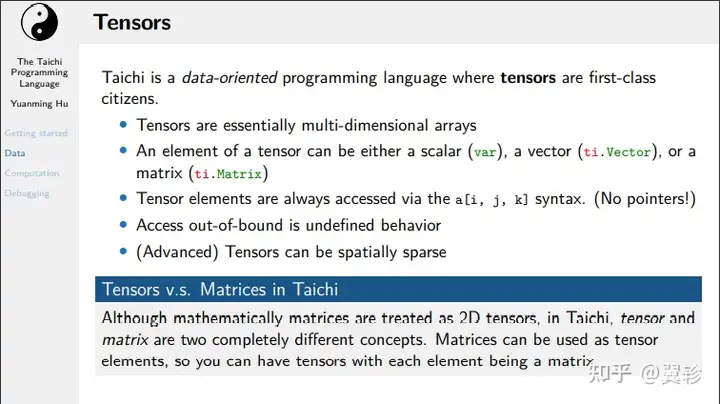
kernels
用于计算的函数,即时编译,kernel不能调用kernel
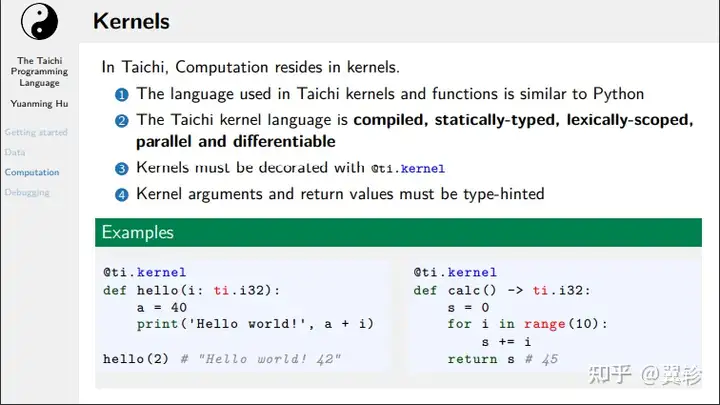
functions
kernel和func均可调用func

标量
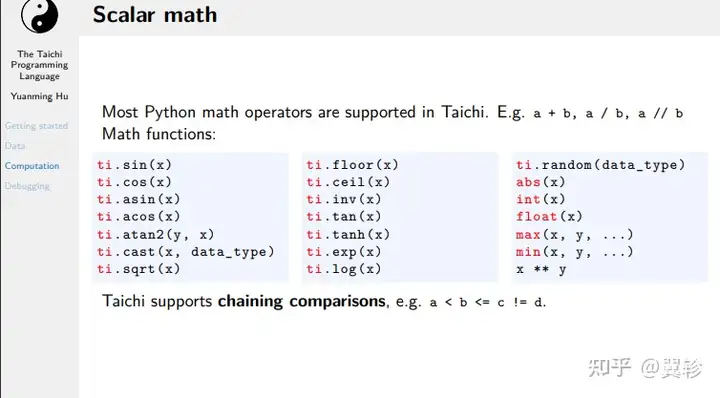
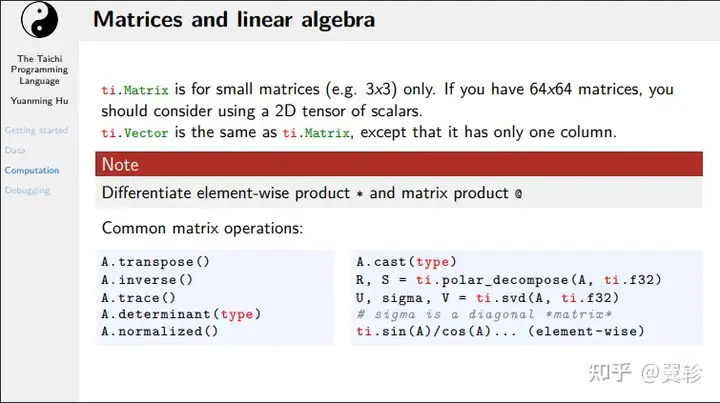
矩阵和线性代数
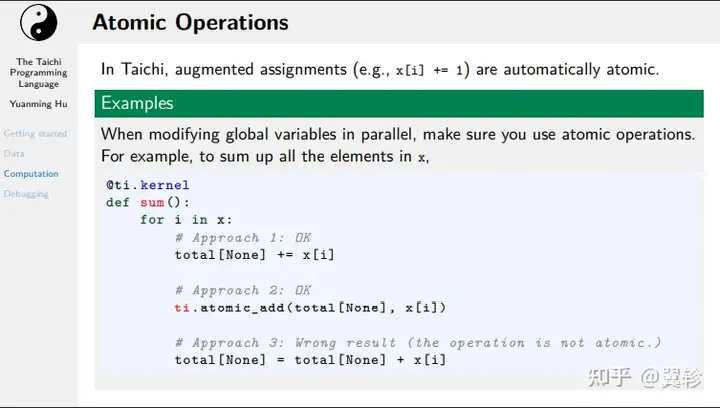
原子操作
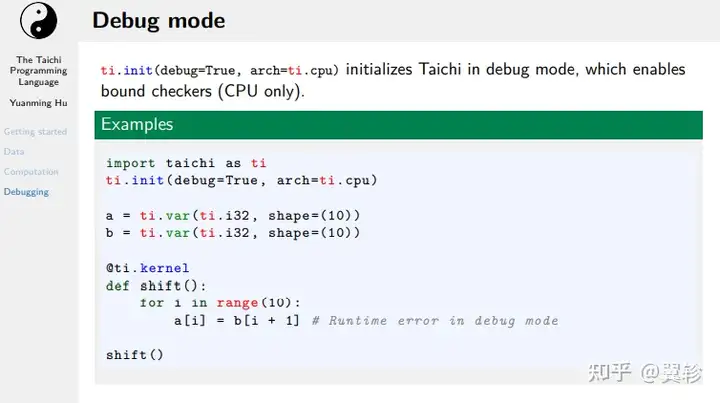
调试
Lec2 拉格朗日视角(1)
介质模拟的两种视角
拉格朗日视角
用拉格朗日粒子、三角网格、方格等代表跟随材料移动的节点,不断检测自身的位置和速度

欧拉视角
网格本身不移动,检测穿过当前节点的材料的速度

两种视角的对比
通常来说,拉格朗日视角很好地体现了“随波逐流”,而欧拉视角更倾向于“岿然不动”

拉格朗日视角下的粒子模拟和欧拉视角下的烟雾模拟

弹簧质点系统
简单但是实用,一般用于布料系统、弹性物体等

系统的理论依据:胡克定律和牛顿第二定律

时间积分
计算机中的时间并不连续,所以需要将时间离散化
前向欧拉,半隐式欧拉,隐式欧拉(经常和牛顿法一同使用)

时间积分器
显式积分:
- 未来的状态只取决于过去的状态
- 容易实现
- 容易爆炸( 需保证约束 )
- 对刚体材料模拟较差
隐式积分
- 未来的状态取决于过去和未来的状态
- 但引入了鸡与蛋孰先孰后的问题
- 难以实现
- 每一步更加费但允许更长的时间间隔
- 会产生一些振荡和死锁问题

实现流程

解线性系统
将上式整理得到线性方程形式,对于大规模矩阵,求解逆矩阵是一个很费的事情,可以使用各种近似方法进行求解。

雅可比迭代(Jacobi iterations):解线性方程的较为简易的迭代法

统一显式与隐式积分器
取不同的值即可得到不同的积分器

平滑粒子流体动力学
使用带有物理量的粒子和kernal函数W来近似连续场(A可以是任何随空间变化的物理量,如密度、压力等。原始的SPH主要被用于天体,也适合处理自由表面流体)

用物态方程做SPH
关键是求解方程(D表示材料导数material derivatives)。流体的运动和流体之间的压强,所受外力有关,所以与压强 、密度以及所受外力 (主要来自重力)有关,压强又可以进一步表示,最终得到一个与密度有关的等式。

根据上述几部分内容,这时就能求出压强的导数,虽然不大准确,但至少对称且满足动量守恒。从而可以使用欧拉法更新下一个时刻的速度与位置。

实现流程

SPH的一些变种
- Predictive-Corrective Incompressible SPH (PCI-SPH)
引入预测机制的隐式积分
- Position-based fluids (PBF)
PBD结合SPH方法
- Divergence-free SPH(DFSPH)
速度上无源场

柯朗-弗里德里希斯-列维条件
该条件用于确定时间步长的上界,在实际使用通过设定值来计算得到时间步长的最大值。

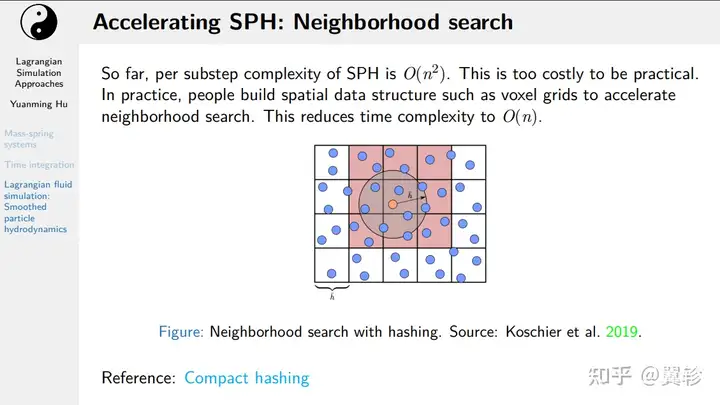
加速SPH:近邻搜索
SPH需要对每个粒子遍历周围的所有粒子,计算复杂度是 O(n^2) ,在实际中可以使用近邻方法进行加速,具体可以使用数据结构(如体素网格等),只在周围的格子里找半径小于h的粒子进行计算,将计算复杂度降至O(nlogn)
其他基于粒子的模拟方法
DEM(Discrete element method):一种离散元素模拟方法,可以用来模拟沙子等
MPS(Moving Particle Semi-implicit):类似SPH,可以更好表现流体的不可压缩性
Power Particles : 视觉上粒子之间的间距会非常均匀

Lec3 拉格朗日视角(2)
弹性与有限元
模拟弹性物体十分有趣
- 不错的视觉表现
- 不难的实现过程
- 许多其他材质的基础(粘弹性, 弹性塑料, 粘塑性…)

形变
形变映射把物体由静止位置映射到形变位置 。将此函数对静止位置求导,得到形变梯度 。

超弹性材料
ψ:势能函数,定义了应力和应变的关系,直观理解为惩罚形变的势函数
应力:材料内部的弹性力,用来恢复材料形状的内力
应变:材料形变的度量,可用形变梯度替换

应力张量
应力代表无限小的材料组件对其周围施加的内力
三种常见的应力张量:P、τ、σ
- P:对ψ求导,在原空间下计算得到应力张量,不对称(易于计算)
- τ:在形变后的空间计算得到,对称
- σ:比较常用,在形变后的空间计算,对称(因为角动量守恒)

常用物理量
- 杨氏模量
- 体积模量
- 泊松比 ∈[0,0.5) (存在负泊松比)
- 拉梅常数 第一常数 (一般用于固体) 第二常数(一般用于液体)

超弹性模型
一般采用Neo-Hookean,形变非常小采用Linear elasticity(旋转后体积无条件变大)

有限单元法
使用连续偏微分方程将空间分为一个个的元素,建立离散

线性三角形有限元
线性三角形有限元(弹性)假定形变映射是仿射的,因此形变梯度在单个四面体单元内是恒定的。

形变梯度F的计算
1.将x拆分为三角形三个顶点a,b,c

2.构建矩阵B和D,并由此构建出矩阵F

显式线性三角形有限元
对每个元素的势能先求导再求和,拆出每个元素的势能,并使用链式求导法则化简替换

隐式线性三角形有限元
式中需要求二阶导数(图与视频有出入)

太极的高级应用
面向对象数据编程

元编程

可微编程

可视化
Lec4 欧拉视角
材料导数
一块材料上物理量的变化取决于时间和空间上的变化

不可压缩的NS方程
速度变化由压强,粘性(一般忽略)和重力加速度三者决定
因为不可压缩,故速度场没有散度

算子分解
先计算平流(速度场的变化),再加上外力,最后由压强进行投影操作,使速度场散度为零


网格结构
均匀网格
将所有信息都存在网格中心

交错网格
相较于均匀网格,交错网格用中心差分离散了压力梯度带来的问题

双线性插值
以面积为权值做双线性插值

平流方案
半拉格朗日平流
基于上一时间步的信息得到这一时间步的物理信息
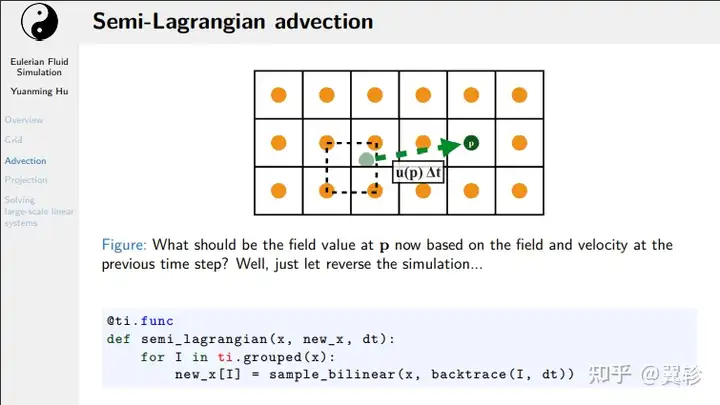
由于速度场并不恒定,物体的移动路径可能非常复杂,用简单的回溯可能会使得到的路径偏离正确路径许多,表现在实际模拟中就是缩小和模糊的问题
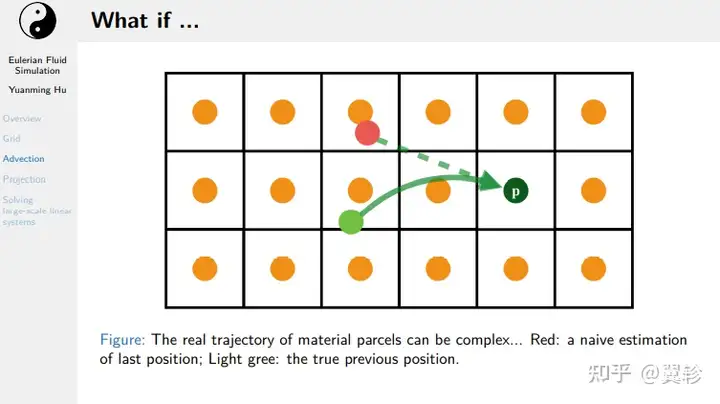
缩小问题:显式中点法
回溯一半,再以此时的速度进行回溯

模糊问题:前后误差补偿和校正
将速度场分别往前和往后推 Δt ,作差后取均得到误差值,将结果加上误差值即可

投影方案
求解标量场使其速度场叠加上其梯度后无散度
克林投影
拉普拉斯算子

泊松方程
中心差分法近似拉普拉斯,先求梯度再求散度

空间离散化

速度场的散度
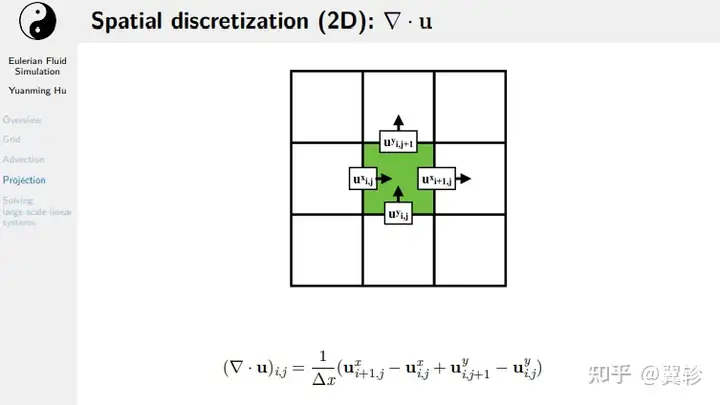
压强的散度

解线性系统
- 直接求解:PARDISO
- 迭代求解:高斯-赛德尔 雅可比 krylov子空间求解

矩阵存储
- 密集矩阵:规模不大时直接存
- 稀疏矩阵:CSR、COO等
- 无矩阵:不存

krylov子空间求解
其中一个最著名的变形为共轭梯度法 conjugate gradients (CG)
其他一些其他在图形学中不常用的方法有CR、GMRES、BiCGStab等



预处理
条件数:一个评价收敛速度的值,越小则收敛越快,等于SPD的最大特征值/最小特征值
减小条件数:找到一个近似的矩阵,且容易求逆。左右同乘逆,此时条件数可能会变小


多重网格方法
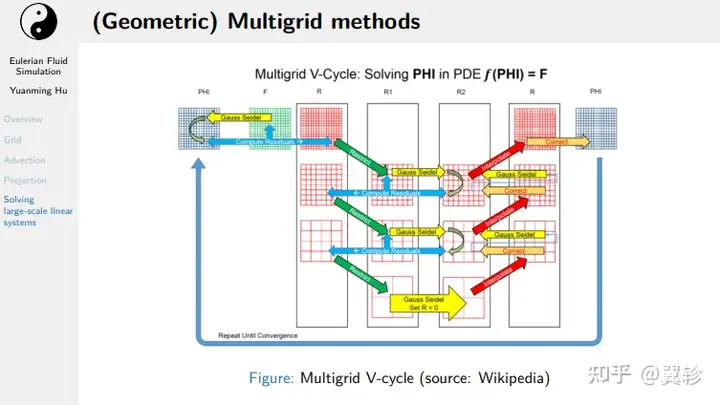


总结摘要

改进方案
修正速度场在经过平流和投影后能量的损失,降低了流体的粘性
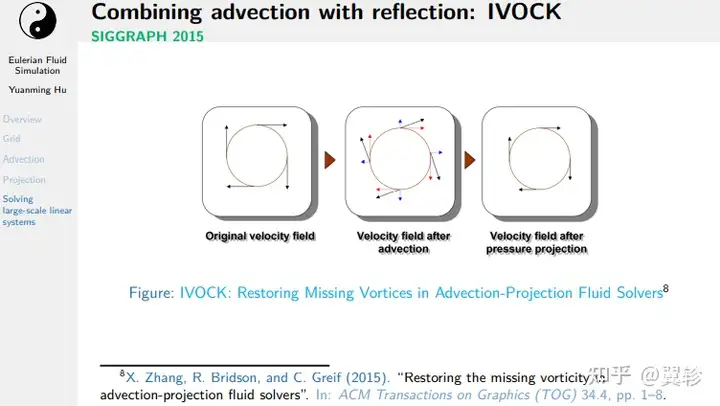
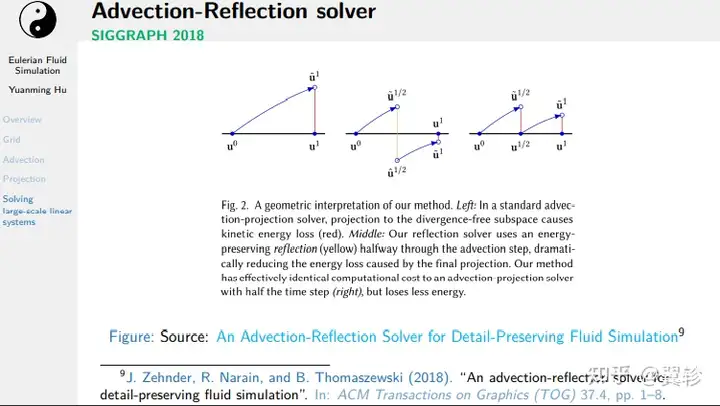
扩展方向
- 从2D到3D模拟
- 精确的边界以及流体固体的耦合
- 两相流体模拟
- 处理自由表面,水平集方法
- 处理涡量守恒

Lec5 线性弹性有限元与拓扑优化
有限元概述
有限元法
有限元法是伽辽金法的一种,将连续型偏微分方程转化为线性系统,用于后续求解
经典步骤:
- 将强型偏微分方程转化为弱型偏微分方程
- 分步积分
- 散度定理进一步简化偏微分方程并得到诺依曼边界条件的显式形式
- 离散化
- 求解线性系统

二维泊松方程
即拉普拉斯方程(泊松方程的简化形式)
- 狄利克雷边界/第一类边界:直接给定边界上的值
- 诺依曼边界/第二类边界: 边界上的值为导数/梯度的值乘以法线方向
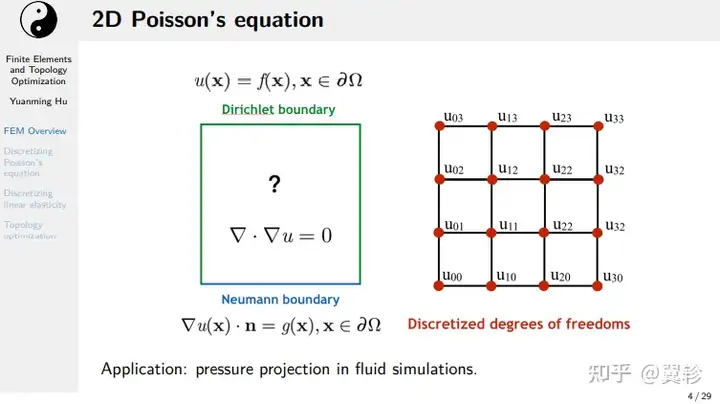
离散化泊松方程
化简
用一个任意的二维标量函数w(x),与强型式∇·∇u相乘,再用w直接与∇u相乘再求导,并展开化简,对两边同时积分化简可得到散度定理:在一个体内对散度的面积分 = 边界上的向量函数和法向量点乘绕边界的线积分



离散
用线性的基函数模拟连续函数,再离散化函数,最后引入矩阵形式



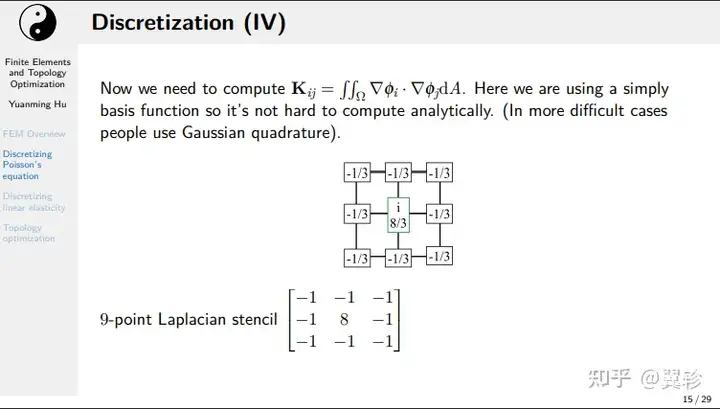

边界条件
用对应的边界条件加以限制

线性弹性有限元
准静态过程下速度很小约为0,重力为0。
自由度: 位移

有限元法求解
用“,”表示求导,αβγ对应xyz轴

将求散度的部分乘以w,再分步积分

离散化w和u

求其中σ和u的线性关系

带入得到线性系统Ku = f

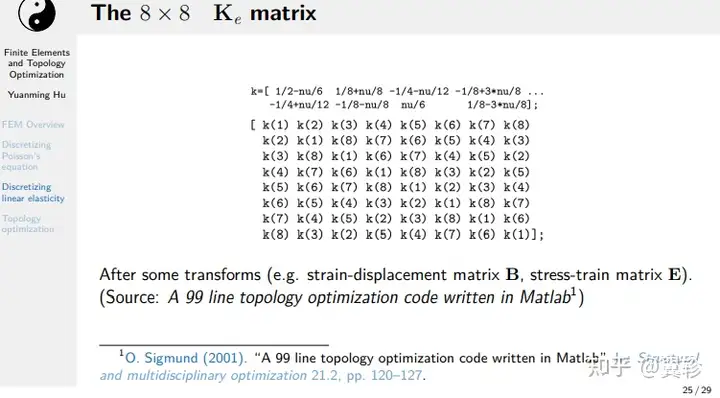
拓扑优化
根据给定的负载情况、约束条件和性能指标在给定的设计区域内对材料分布进行优化,是结构优化的一种。

Lec6 混合欧拉-拉格朗日视角(1)
欧拉法和拉格朗日法对比
衡量模拟质量的因素
- 物理属性:动量/角动量/体积/能量
- 性能:并行性/访存
- 复杂度

欧拉法和拉格朗日法对比
欧拉法在投影阶段优势:
- 易于离散化拉普拉斯算子
- 查找邻居信息效率高
- 易于预处理,使收敛速度变快
欧拉法在平流阶段缺点:
容易损失能量以及丢失几何细节

拉格朗日法在平流阶段优势:
- 易于移动位置
- 易于满足守恒(低耗散)
拉格朗日法在投影阶段缺点:
- 不容易离散化
- 需要复杂的数据结构查询邻居信息

混合欧拉-拉格朗日法
混合欧拉-拉格朗日法步骤
- 粒子转网格:把粒子上的信息存储到欧拉网格上
- 网格操作:把速度的散度分量利用投影消除(不可压缩),应用边界条件
- 网格转粒子:信息从欧拉网格到粒子
- 粒子操作:移动粒子,更新材料的形变、梯度、体积等其它属性
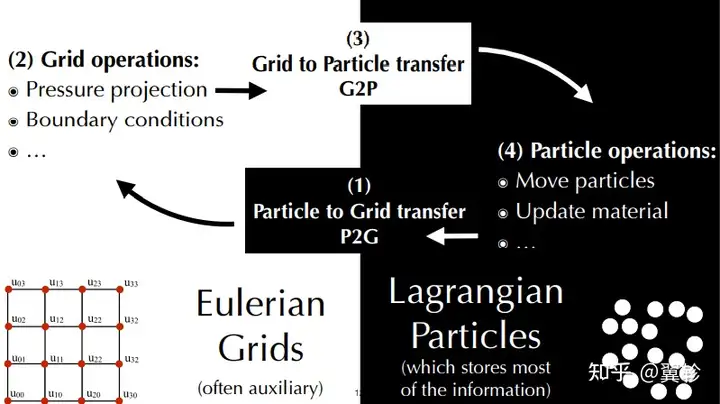
质点网格法(PIC)
质点网格法中的粒子网格互转:二维范围内,属性给到周围3x3的网格,按照距离远近使用核函数计算权值
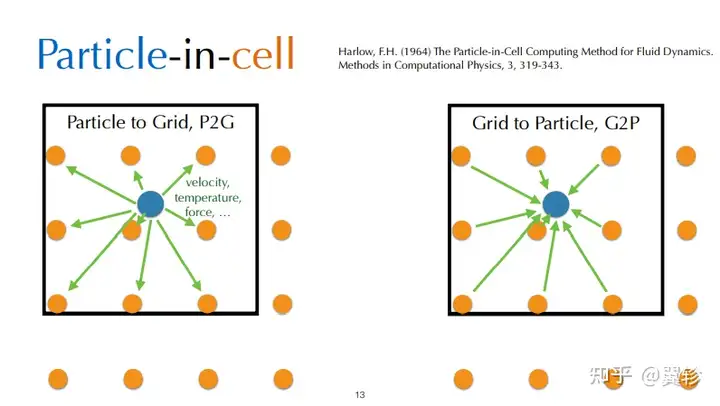
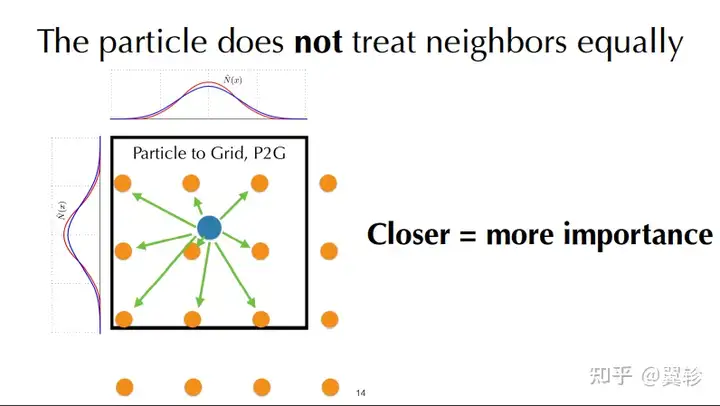
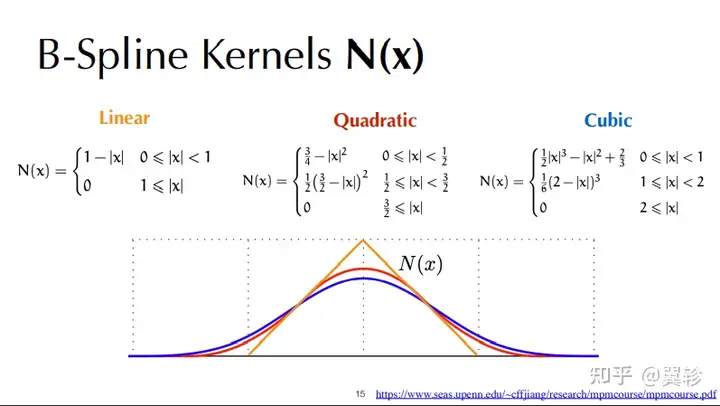
质点网格法和泊松求解器结合
模拟步骤:
- 粒子转网格:将速度从粒子散入网格
- 在网格上求解压力,并经过投影阶段更新速度场
- 网格转粒子:从速度场网格得到粒子速度,更新粒子的位置

问题:能量耗散,流体过粘
原因:网格转粒子阶段信息丢失,18自由度变成2自由度

改进:
- 传输更多的信息:APIC,PolyPIC
- 只传输增量:FLIP

仿射粒子元胞法(APIC)
在速度场的基础上增加了一个仿射场,使粒子的自由度由2个增加到了6个,保证了角动量守恒
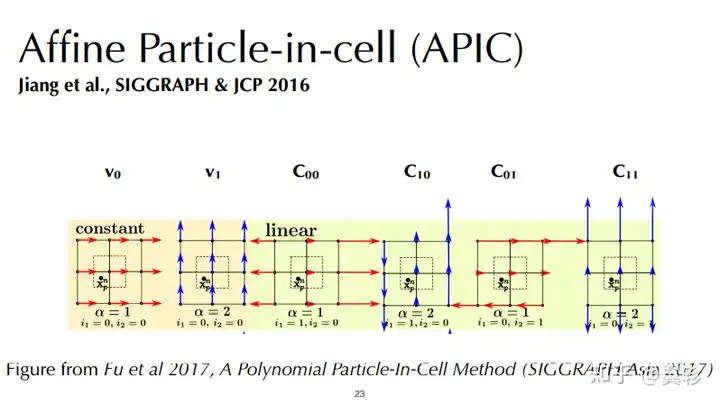


多项式质点网格法(PolyPIC)
在APIC的基础上,粒子的自由度从6个增加到18个(理论上能在网格和粒子的转化中不丢失任何信息)
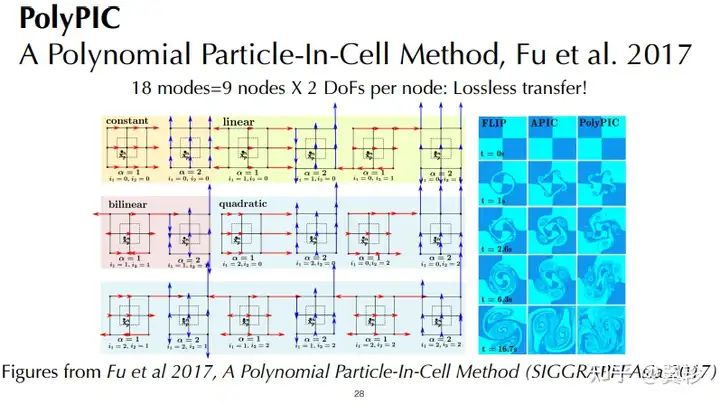
隐式流体粒子(FLIP)
在网格和粒子相互转化的过程中,只传递物理量的增量而非物理量本身
缺点:噪声大,且需要额外的空间存储网格再计算差值

PIC能量耗散大,FLIP噪声大,将两者结合起来,可以达到能量耗散不大且噪声变小的效果
FLIP0.99 = 0.99 * FLIP + 0.01 * PIC

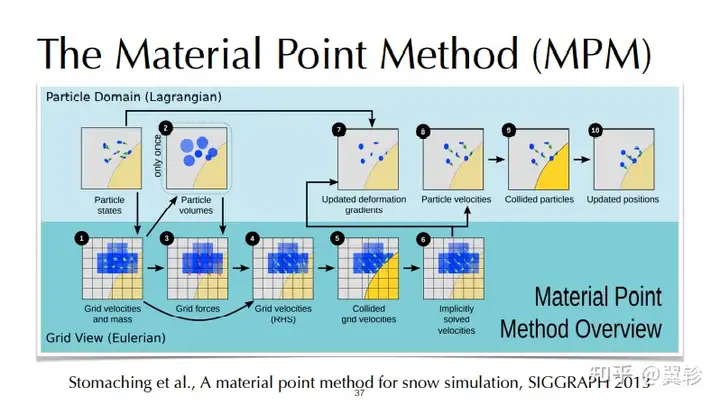
物质点法(MPM)
较好的混合欧拉-拉格朗日法的模拟方案,粒子存储了速度、形变梯度、体积等物理量


MPM法流行的原因:
- 耦合了不同的物理材料
- 处理碰撞和自碰撞
- 材料断裂的处理
- 模拟大形变


Lec7 混合欧拉-拉格朗日视角(2)
移动最小二乘物质点法(MLS-MPM)
仿射粒子元胞法(APIC)
对比PIC额外维护了变量C(2x2或3x3的矩阵),记录了粒子周围的仿射速度场(ax+b中的a项)
- 粒子转网格:求网格上的动量和质量,其中增加仿射的部分
- 网格操作:从动量求出速度,求解泊松方程得到无散的速度场
- 网格转粒子:将速度转到粒子上,更新粒子位置,求新的矩阵C

移动最小二乘物质点法(MLS-MPM)
对比APIC改进的地方:
- 粒子转网格:将形变梯度引入动量的计算,增加了一个弹力项
- 网格操作:计算弹性物体时,压力投影替换为边界条件的约束计算得到速度

计算形变梯度
使用矩阵C近似了速度的梯度

计算内力
其中f为对弹性势能求导
- 代入势能公式
- 对x估值的求导等于对速度的求导乘以τ
- 链式求导法则带入对F和C的求导
- 求导
- 化简


网格操作
在网格上边做分步积分和应用散度定理
边界类型:
- 粘性边界,速度归零
- 滑移边界,靠近和离开边界时均有阻力
- 分离边界,只在靠近边界时存在阻力
其他情况:
- 重力对速度的作用,施加在边界计算之前
- 包含其他碰撞的物体时,取相对速度
- 边界的摩擦

MLS-MPM对比MPM的优点
- 重用APIC的C矩阵作为形变梯度中∇v的近似,减少了浮点运算
- 将形变的更新从网格转粒子阶段提前到粒子转网格阶段,减少了带宽消耗
- 在粒子转网格计算动量时,其中APIC和MLS-MPM的动量项可以合并,节省了浮点运算

本构模型
一些在框架下实现的材料模型:弹性物体,流体,弹塑性物体(雪、沙等)
本构模型实现时需要注意的点:形变更新、压强计算

弹性体

流体
用体积变化比求压强P,得到柯西应力
数值不稳定性:在求行列式时,可能出现精度问题(常见于流体模型)
避免方案:在粒子中增加对J的存储,而非使用形变梯度F求出新的J

使用弹性模型,把参数µ设置为零

弹塑性体
- 更新弹性形变梯度
- 求奇异值分解矩阵
- 裁剪掉Σ中拉伸和压缩超出范围的值
- 用裁剪后的Σ作为弹性形变梯度,裁剪掉的值作为塑性形变梯度

物质点法中的拉格朗日力
将物质点法中的粒子作为有限元法的顶点,计算采用有限元法的势能模型,不再需要计算形变梯度
- 对比有限元法:能处理自碰撞
- 对比物质点法:由于使用了纹理而不是网格,避免物质点法中由于采样密度不够高导致的数值断裂
- 更容易耦合物质点法和有限元法









