Written before

  Reading engine source code is fundamental for engine development roles, and those who know me are aware that I focus on physics simulation. During an internship at a project team, I had modified Unity’s source code, but back at school, I can only access open-source engines. UE’s Chaos is somewhat heavy: during initialization, the Scene sequentially creates Scene, Solver, Evolution, and Objects sequentially register events, create states, and initialize bodies; during simulation, AOS data from the game thread is pushed to the SOA physics thread, undergoes a series of complex calculations (considering my focus on mobile performance), and then dirty modified data is pulled back. In contrast, Godot’s source code is lightweight and well-structured, making it suitable for dissecting the 3D physics portion.

  Reviewing the latest Godot 4.5 documentation is actually quite interesting. For example, Godot’s memory management: small objects use heap allocation with reserved free memory, while large objects use a dynamic memory pool (recorded using PooledList for lists and freelists). This differs significantly from the OS’s paging choices, highlighting the difference between specialization and generality? Also, Godot’s 2021 article explaining why it doesn’t use an ECS architecture and its choice of abstraction levels (offering a new perspective, though I personally don’t entirely agree, but since it’s open source, one can build their own framework if needed). Furthermore, Godot’s mobile rendering pipeline cannot read adjacent pixels (Seriously? This disables fragment derivatives, and compute shaders are largely unsupported. Even phones in India and Southeast Asia aren’t this fragile, are they?).

Architecture Overview

  The entire 3D physics portion of Godot resides in modules/godot_physics_3d, making it exceptionally convenient to locate.

  • Physics Server (godot_physics_server_3d) creates and manages spaces, shapes, areas, and collision objects.
  • Physics Space (godot_space_3d) contains all objects in the physics world and is responsible for physics simulation.
  • Physics Stepper (godot_step_3d) is used by the space to step through the physics simulation.
  • Collision Detection (godot_broad_phase_3d) quickly identifies potential colliding object pairs.
  • Collision Solver (godot_collision_solver_3d) handles specific collision detection between shapes.
  • Shapes (godot_shape_3d) define various geometric shapes used for collision detection.
  • Collision Objects (godot_collision_object_3d) are the base classes for Areas, RigidBodies, and SoftBodies, all of which can have shapes.
  • Areas (godot_area_3d) detect object entry and exit and can modify properties like gravity.
  • Rigid Bodies (godot_body_3d) are hard physical objects affected by forces and collisions.
  • Soft Bodies (godot_soft_body_3d) are deformable objects simulated using a particle system.
  • Constraints and Joints (godot_constraint_3d and godot_joint_3d) restrict motion between objects.

  The simulation flow is roughly as follows:

img

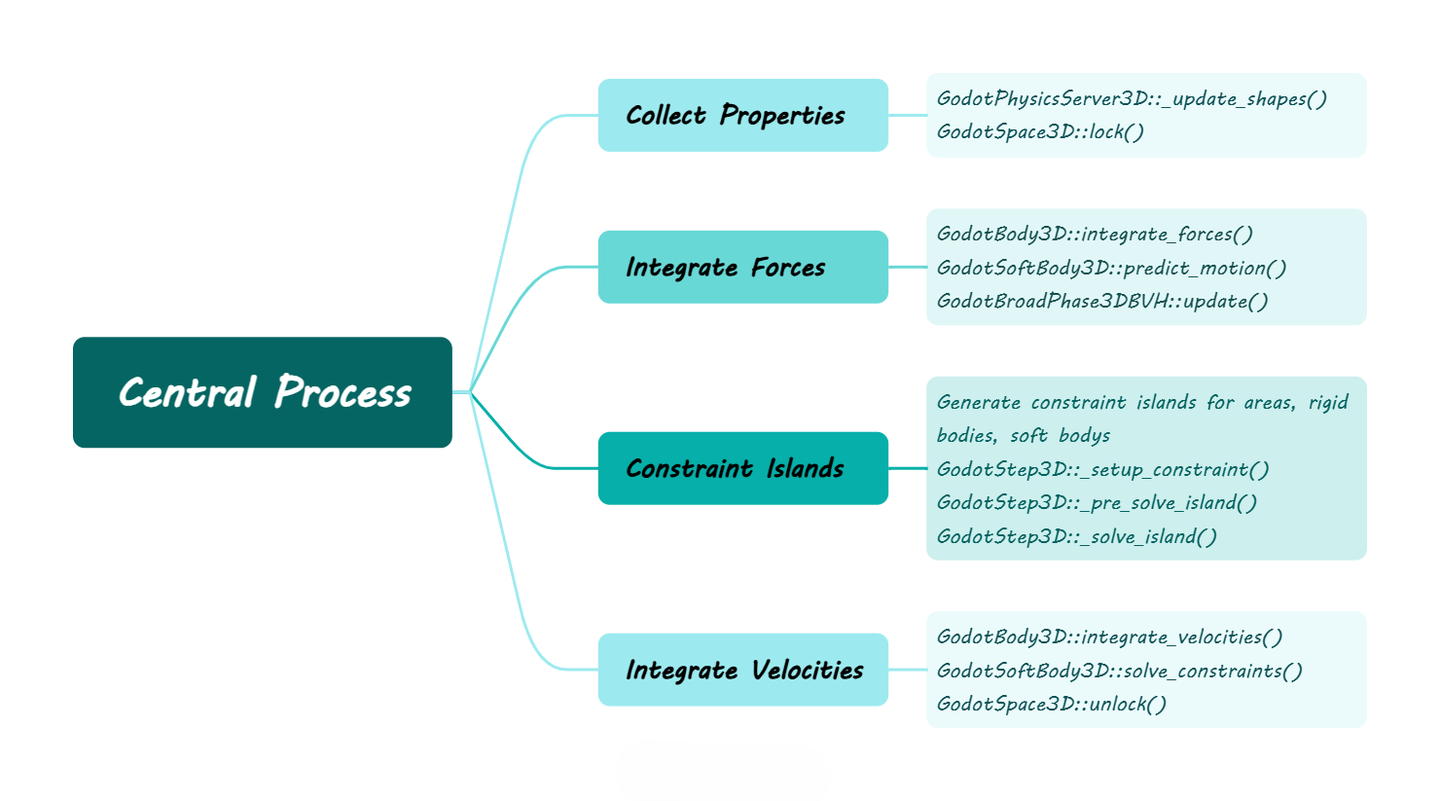
Parameter Preparation

  First, let’s start with preparation. Although it involves handling various property settings, the main processing lies in updating the object’s mass properties. Taking the most complex RigidBody as an example, it first calculates the total area (summing the area of each shape), then calculates the center of mass (distributing mass proportionally by area), and finally calculates the inertia tensor (parallel axis theorem).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void GodotBody3D::update_mass_properties() {
    // Select the calculation path based on the mode type
    switch (mode) {
        case PhysicsServer3D::BODY_MODE_RIGID: {
            // Rigid body - Complete calculation of mass properties
            // Area - Mass Center - Inertia
        } break;
        case PhysicsServer3D::BODY_MODE_KINEMATIC:
        case PhysicsServer3D::BODY_MODE_STATIC: {
            // Kinematics/Static Body - No Mass Attribute
        } break;
        case PhysicsServer3D::BODY_MODE_RIGID_LINEAR: {
            // Linear rigid body - Mass only, no rotational inertia
        } break;
    }
    
    // Update the quality attributes of the dependency transformation
    _update_transform_dependent();
}

  Let’s briefly supplement the calculation of the inertia tensor:$I_{total} = \displaystyle\sum_{i=1}^{n}{(R I_{local}R^T + w(r \cdot r \cdot I_{identity} - r \otimes r))} $。Bounded by the plus sign, the left side is the current shape’s moment of inertia, and the right side is the weighted composition. This might be abstract, so let’s illustrate with the inertia tensor of a point cloud.

  Assume we have a spinning top composed of n points, where the coordinates of point i are pi, the mass of point i is mi, and we wish to calculate its initial rotational inertia. Then the formula is:$I_{ref}=\displaystyle\sum_{i=1}^{n}(m_i(r_i\cdot r_i\cdot I_{identity}− r_i\otimes r_i))$，, where the offset vector $r_i=p_i-p_{center}$. This is the right part of the formula used by the engine, where the dot product describes mass distribution, and the outer product describes inertia contribution. Then the top starts spinning with rotation matrix $R$, giving $ I=RI_{ref}R^T $. This is the left part of the formula. Combining them yields the scheme used by the engine (here, the engine’s method accounts for the positional offset of the shape within the overall inertia tensor, which I personally find unnecessary).

Integrating Forces

  After updating the physical properties, the next steps are integrating external forces for rigid bodies, shape prediction for soft bodies, and BVH collision detection.

Integrating Forces for Rigid Bodies

  First is integrating forces for rigid bodies. Skipping the code that iterates through areas to determine damping modes, we go directly to the core part. For kinematic objects, they are externally driven, and their linear and angular velocities are updated based on position and rotation changes. For rigid bodies, they first calculate the net force and net torque, then apply damping to update velocity.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void GodotBody3D::integrate_forces(real_t p_step) {
	if (mode == PhysicsServer3D::BODY_MODE_STATIC) return;

	// Get current gravity and damping 

	if (mode == PhysicsServer3D::BODY_MODE_KINEMATIC) {
		//compute velocities from prev transfor
	} else {
                //compute force and torque
                //apply damp and update velocity
		}
		//If CCD is used, calculate the motion for this step.
	}

	//If motion is calculated, update the shape for ray cast.
}

Shape Prediction for Soft Bodies

  Next is shape prediction for soft bodies. Similarly, skipping the code that iterates through areas to determine gravity, after calculating wind forces, the integration uses explicit Euler plus displacement clamping, and finally updates bounds and acceleration structures (AABB bounding box tree). (The soft bodies don’t even use semi-implicit Euler, but the subsequent iterative correction for soft bodies should suffice.)

1
2
3
4
5
void GodotSoftBody3D::predict_motion(real_t p_delta) {
	// Apply gravity and wind forces.
	// Explicit euler + displacement clamping
	// Update AABB bounds tree(vertices and triangular faces).
}

BVH Collision Detection

  Finally, BVH collision detection: first update the BVH tree, then detect collisions. Updating the BVH tree involves incremental optimization and dynamic expansion. The collision detection phase first expands AABBs, then fills clipping parameters, identifies items no longer colliding, queries overlapping items, and processes new collisions.

1
2
3
4
void GodotBroadPhase3DBVH::update() {
        // Update BVH tree
        // Check collisions
}

  Starting with Godot’s implementation of a dynamic BVH tree based on a template library, node and leaf definitions are as follows.

1
2
3
4
5
6
7
8
9
10
11
12
13
struct TNode {
    BVHABB_CLASS aabb;
    union { int32_t num_children, neg_leaf_id; };
    uint32_t parent_id;
    uint16_t children[MAX_CHILDREN];
    int32_t height;
};

struct TLeaf {
    uint16_t num_items, dirty;
    uint32_t item_ref_ids[MAX_ITEMS];      // Array of item reference IDs
    BVHABB_CLASS aabbs[MAX_ITEMS];         // Array of item AABB
};

  In incremental optimization, it starts from the bottom-up to update AABB bounding boxes based on the existing structure, then extracts a node per frame to update and reinsert it, thus solving AABB inflation and suboptimal placement.

1
2
3
4
5
6
7
8
void incremental_optimize() {
	// Traverse downwards to the leaf nodes.
	// Check for dirty marks, if necessary do upward fit.
        refit_branch(root);
        // Remove and get AABB
        // Reinsert and balanced the path
        _logic_item_remove_and_reinsert(node)
}

Constraint Grouping

Constructing Constraints

  After integrating external forces, the next step is constructing constraint relationships for subsequent parallelization. Godot divides this into three different logics for Areas, RigidBodies, and SoftBodies. Simply put, the Area part just throws any associated object in (since no computation is performed). RigidBodies detect associated RigidBodies and SoftBodies. SoftBodies only detect associated RigidBodies (SoftBody-to-SoftBody collisions are presumably not supported yet). The logic for constructing constraints in these three parts is largely similar; here, we show the RigidBody’s as a simple example.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
void _populate_island(GodotBody3D *p_body, ...) {
        // 1. Iterate through all the constraints of the rigid body
        for (const KeyValue<GodotConstraint3D *, int> &E : p_body->get_constraint_map()) {
        
        // 2. Search for the connected rigid body
        for (int i = 0; i < constraint->get_body_count(); i++) {
            GodotBody3D *other_body = constraint->get_body_ptr()[i];
            if (i == E.value) continue;  // Skip self
            _populate_island(other_body, ...);  // Recursive detection
        }
        
        // 3. Search for the connected soft body
        for (int i = 0; i < constraint->get_soft_body_count(); i++) {
            GodotSoftBody3D *soft_body = constraint->get_soft_body_ptr(i);
            _populate_island_soft_body(soft_body, ...);  // Turn to softbody
        }
    }
}

Solving Constraints

  After constructing constraints, the next step is solving them: first, set up all constraints in parallel, then pre-solve on a single thread (filtering invalid constraints), and finally solve in parallel (using prioritized iterations). Specific constraints are implemented by inherited classes like area, body, joint. Here, we analyze the more generic body (area has no solving step, and joints have too many variants).

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
bool GodotBodyPair3D::setup(real_t p_step) {
         // 1. Check exception layers and collision layers
         // 2. Calculate offset
         // 3. Detect collisions
         // 4. Mark whether CCD is required
}

bool GodotBodyPair3D::pre_solve(real_t p_step) {
         // 1. If CCD is required, call _test_ccd()
         // 2. Calculate the quality, offset, and impulse of the contact point
         // 3. Report the contact point
         // 4. Calculate the rebound coefficient
}

void GodotBodyPair3D::solve(real_t p_step) {
         // 1. Solving for the offset impulse (for penetration resolution)
         // 2. Solving for the normal impulse (for collision resolution)
         // 3. Solving for the tangential impulse (for friction resolution)
         // 4. Accumulating and limiting the impulses
}

  It’s worth noting that its 3D collision detection is a port of the GJK-EPA algorithm from the Bullet physics engine, a standard in game engines. However, I’m curious why no engine implements SAT. This O(n) algorithm with a small constant might be better than O(log n) with a large constant for simple shapes like OBBs, especially within 100 items. The reason might be that Godot needs EPA to calculate depth for penetration impulses, but I personally dislike the non-physical concept of penetration impulses. I guess I’ll have to write my own physics engine to play with it someday.

Integrating Velocities

Integrating Velocities

  After solving constraints, the next step is integrating velocities. For rigid bodies, this essentially involves various callback registrations, handling object properties, and updating positions with axis locking.

1
2
3
4
5
void GodotBody3D::integrate_velocities(real_t p_step) {
         // 1. Callback registration
         // 2. Kinematic objects, axis locking processing
         // 3. Transformation update
}

Constraint Solving

  For soft bodies, the final output stage is slightly more complex, involving iterative constraint solving (essentially based on PBD distance constraints but with XPBD-like stiffness scaling and mass weighting).

1
2
3
4
5
6
void GodotSoftBody3D::solve_constraints(real_t p_delta) {
         // 1. Pre-compute link parameters
         // 2. Predict position (using current speed)
         // 3. Iteratively solve constraints (position correction)
         // 4. Update physical properties
}

  Let’s briefly expand on constraint solving. It first calculates compliance $c_0 = (invMass0 + invMass1) / stiffness$, then solves with $k = (L² − |x|²) / (c0 ∗ (L² + |x|²))$. The first step combines mass and stiffness but does not divide by $Δt²$ to decouple material properties from simulation timestep. The second step uses $(L² + |x|²) $in the denominator for numerical stability but does not store and accumulate Lagrange multiplier λ, so it’s only a modified PBD.

  But then again, in games, timestep and iteration counts are constant; as long as stiffness is adjustable, it’s fine. Not to mention the 5%-10% performance cost from XPBD, XPBD is also burdened by the large constant $Δt²$, making parameter adjustment non-intuitive. For artists, tweaking parameters to extreme values only yields subtle differences. In such cases, XPBD becomes a technical trap (since I handle programming, design, and art).

Summary

  Godot’s 3D physics engine is a lightweight, modular real-time physics simulation system. Through constraint partitioning and parallel solving, it can also run efficiently on multi-core CPUs. Although reading source code is inherently troublesome, it’s far less mentally taxing than UE. I hope this analysis provides some help to readers.